Построение отрезка равного числу Пи и решение квдратуры круга

Геометрия, как наука, начала формироваться около четырех тысяч лет назад и явилась следствием потребности древнего человека в решении практических задач: возведения сооружений и землеустройства. Античные геометры  верили в неограниченные возможности циркуля и линейки пока не столкнулись с построением некоторых правильных многоугольников  и тремя ставшими впоследствии знаменитыми задачами древности (удвоении куба, трисекции угла и квадратуры круга).

В 1882 году немецкий математик Ф. Линдеман, опираясь на работы своих предшественников И. Ламберта, А. Лежандра, Ш. Эрмита, вывел строгое доказательство трансцендентности числа Pi. Таким образам было окончательно установлена невозможность точного построения квадрата равновеликого кругу циркулем и линейкой.

Приводимое ниже построение отрезка равного числу Pi, исходя из радиуса окружности, не противоречит выше изложенному материалу. Древние геометры Антифон, Бризон, Архимед нашли геометрическое решение вычисления числа Pi, суммированием сторон правильных вписанных в окружность или описанных вокруг нее многоугольников. При неограниченном возрастании количества сторон многоугольника, его периметр становится в пределе соизмеримым с длинной окружности. Аналогично сказанному, построенный предлагаемым здесь методом отрезок, гораздо быстрее стремится к длине полуокружности, т.е. числу Pi, нежели периметр многоугольника.

Длина окружности определяется формулой L = 2(Pi)R, площадь круга соответственно S = (Pi)R^2. Если радиус, какого либо круга принять за единицу, тогда его площадь можно выразить прямоугольником, стороны которого равны Pi и R. В этом случае, большая сторона прямоугольника равна длине полуокружности, а малая - единичному отрезку. Среднее геометрическое сторон прямоугольника есть сторона квадрата равновеликого исходному кругу, точное построение которого можно осуществить известным способом. Таким образом, решение квадратуры круга сводится к построению отрезка равного Pi, вариант которого предлагается ниже.

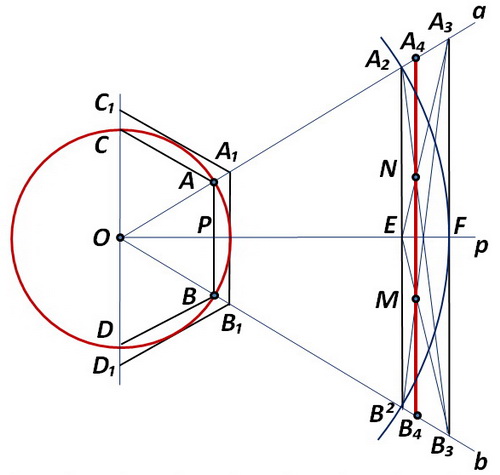
Очертим окружность произвольным радиусом R, центр которой обозначим точкой О. Впишем в окружность и опишем вокруг нее правильные шестиугольники. На рисунке изображены по три стороны от этих многоугольников, опоясывающих полуокружность, с целью разъяснения материала. В построении участвует одна сторона АВ от вписанного шестиугольника. Проведем три луча Оа, Оb и Op, исходящих из центра окружности и проходящих через концы отрезка АВ и его середину, точку Р. Опишем дугу из точки О как из центра раствором циркуля в три раза большим за радиус исходной окружности. Дуга пересечет лучи в точках А2, F, В2. Построение можно осуществлять от любого другого вписанного в окружность правильного n-угольника. В этом случае радиус дуги определятся выражением r = nR/2.

Стянем прямой точки А2 и В2. Построенный отрезок равен полусумме сторон вписанного шестиугольника А2В2 = СА + АВ + BD, с недостатком относительно длины полуокружности. Далее построим отрезок А3В3, проведением прямой параллельно А1В1 через точку F, до пересечения с лучами Oa и Ob. Он имеет длину соответствующую половине сторон описанного шестиугольника А3В3 = С1А1 + А1В1 + В1D1, с избытком относительно полуокружности. Таким образом, расположение отрезка равного длине полуокружности следует искать на участке меду отрезками А2В2 и А3В3.

Для этой цели воспользуемся следующим способом. Стянем прямыми концы построенных отрезков крест накрест. Точку E, образованную пересечением отрезка А2В2 и луча Op, соединим с точками А3 и В3. В результате новые отрезки в местах пересечения образуют точки M и N. Построим отрезок А4В4, проходящий через эти точки. Сколь верно он соответствует длине полуокружности (числу Pi) можно узнать, проведя вычисления по формулам:

b = (1 –(a/2)^2)^(1/2), (b - высота треугольника OP),

А4В4= an(1 + (1 –b)/(2 + b))/2.

Здесь a - длина стороны вписанного в окружность многоугольника, а n – число его сторон.

На представленном иллюстрацией построении А4В4 = 3,14023…, что примерно соответствует значению полученному Архимедом. Но он достиг данного результата вычислением периметров описанного и вписанного в окружность 96-ти угольника. Воспользуемся предлагаемым методом и проведем построение на стороне 96-ти угольника. Тогда длина отрезка А4В4 = 3,1415926335… с точностью в семь знаков после запятой.

Использование указанных формул позволяет получать в два раза больше точных цифр относительно метода Архимеда. Например, периметр вписанного многоугольника состоящего из 96304 сторон дает значение Pi с точностью в десять знаков, а новый метод – в двадцать. Данная тенденция сохраняется при дальнейшем увеличении сторон многоугольника. Следовательно, с точки зрения теории, точность построения ничем не ограничена.

/Стрижак Василий Васильевич/ г.Речица, Гомельская обл.