Иллюстрация классических средних величин

Античные математики, увлеченные изучением пропорций, подразделяли их на три вида: арифметическую a – b = c – d; геометрическую a / b = c / d; гармоническую 1/a – 1/b = 1/c – 1/d. Особый интерес имели пропорции, у которых средние члены были равными b = c. Тогда, переобозначая  b и c через m, g или h,  получали  для средних величин следующие выражения: арифметическое среднее m = (a + d)/2; геометрическое среднее g = (ad)^(1/2); гармоническое среднее h = 2ad/(a + d).                   

Следует заметить, пифагорейцы, постигая средние с позиции математических  свойств, вкладывали в них определенный смысл. Так отрезок m представлялся арифметически, то есть меньшим за a и большим  d  на одну и ту же величину. Отрезок g – геометрически, стороной квадрата равновеликого прямоугольнику со сторонами a и d. Среднее гармоническое понималась как среднее арифметическое обратных величин. Все эти средние для двух положительных чисел a и d, принято считать классическими. К ним относится четвертое среднее – квадратическое: по определению неотрицательное число, квадрат которого есть среднее арифметическое квадратов чисел а и d, т. е. число s = ((a^2+d^2)/2)^(1/2).

Важность средних величин с течением времени постоянно повышалась в связи с развитием новых методов статистики и теорий вероятностей. Решение целого ряда практических и теоретических задач невозможно осуществить без применения средних. Отображение классических средних на геометрическом рисунке дает наглядное представление об их величине относительно заданных отрезков. В литературе по математике имеются построения средних величин, но в них отсутствует тесная взаимная связь. Рассмотрим вариант, в котором отрезки заданных и средних величин объединены одной общей точкой. В этом случае их иллюстрация позволяет визуально оценить гармонию средних.

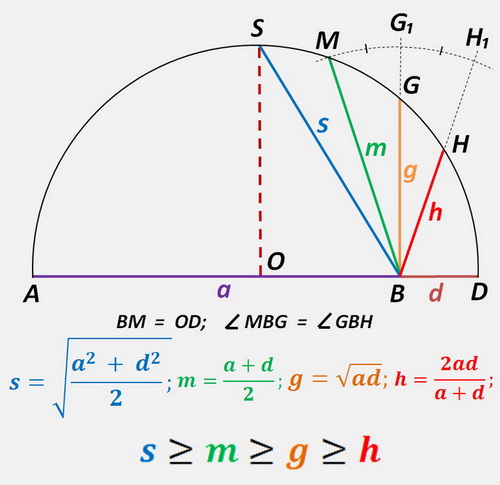
На прямой отложим последовательно два исходных отрезка а = АB и d = BD. Из середины АD (точки О), как из центра, проведем полуокружность радиусом ОА. Из точки В не изменяя раствор циркуля сделаем засечку на полуокружности в точке M. Соединим точки B и M прямой. Отрезок BM отображает m - среднее арифметическое. Восстановим два перпендикуляра из точки B и О до пересечения с полуокружностью соответственно в точках G и S. Тогда BG – среднее геометрическое g по построению. Среднее квадратическое s получим соединением точек B и S. Отрезок BH равный среднему гармоническому h построим, как показано на рисунке, т.е. с учетом равенства углов MBG и GBH.

Таким образом, все средние выходят из одной точки B веером, достигая полуокружности. Если исходные отрезки a и d значительно отличаются по длине, то точка B, разделяющая их, расположится ближе к краю диаметра, «веер» средних станет шире с увеличением разности между ними. В случае, когда точка B окажется недалеко от середины диаметра, все будет наоборот – «веер» средних сузится и как следствие разность между ними сократится. При равенстве отрезков a и d все средние сольются в один общий отрезок OS.

/Стрижак Василий Васильевич/ г. Речица, Гомельская обл.